What is Attention?
Attention
注意力的来源或许是因为大数据,在大数据中什么样子的数据都有,对于重要的数据我们要使用,对于不太重要的数据我们需要暂时忽略。
但是对于主流的卷积神经网络(Convolutional Neural Networks, CNN)或短期记忆递归神经网络(Long Short-Term Memory, LSTM)很难去决定什么重要,什么不重要。
在2017年Google发布 Attention is All You Need 前就已经有人发现了如何在深度学习的模型上做注意力,再后来注意力就诞生了。
人类的视觉注意力
Attention翻译成注意力,从其的命名方式来看,很明显借鉴了人类的注意力机制,因此,我们首先介绍人类的注意力
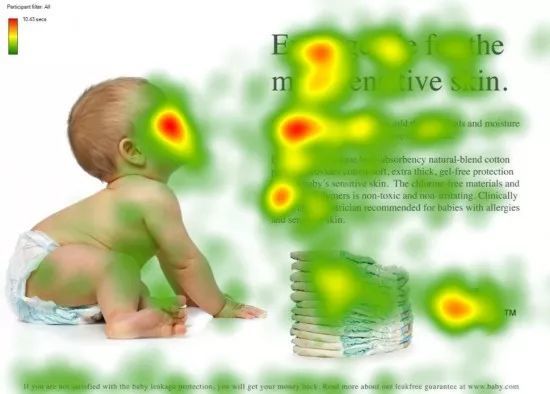
我们看到这张图,研究员发现,当一个人看到这张图时,他/她的眼睛会聚焦到红色的区域。
我们分解以下可以得到以下信息:
- 人看脸
- 文章看标题
- 段落看开头
研究员们发现,这些红色的区域往往可能包含着重要的信息。
**注意力机制:**我们会把我们的焦点聚焦在比较重要的事物上。
怎么做注意力?
回到刚才的那张图,存在着两个对象:
- 我(查询对象$Q$)
- 图(被查询对象$V$)
当我们看到这张图的第一眼,我们就会开始去判断哪些事物对我而言重要和哪些事物对我而言不重要,其实就是去计算$Q$和$V$里的事物的重要度。
重要度计算其实就是相似度计算,就是计算$Q$和$V$里面的事物哪些更接近?
以下我们使用点乘的方式去进行相似度计算。
$Q$, $K = K_1,K_2,\cdots,k_n$
我们的$K$包含了很多的事物,如上述式子,通过点乘的方法计算$Q$和$K$里的每一个事物的相似度,就可以拿到$Q$和$K_1$的相似值$a_1$,$Q$和$K_2$的相似值$a_2$,$Q$和$K_n$的相似度$a_n$。
Tips:点乘其实就是求内积,在此我们无需知道为什么它能求内积
再拿到相似度后,我们做一层$Softmax(a_1,a_2,\cdots,a_n)$就可以得到概率。
进而就可以找出哪个对于$Q$而言就更重要。

对于我们获得的所有的概率值我们还需要进行汇总,当你使用$Q$查询结束后,$Q$已经失去了它的使用价值了,而我们最终拿到的是一张多了一些信息的图片(多了于我而言更重要和更不重要的信息)。
在$(a_1,a_2,\cdots,a_n)*(v_1,v_2,\cdots,v_n) = (a_1 * v_1+a_2 * v_2+\cdots+a_n * v_n)$
这样之后就得到了一个新的$V$,这个新的$V$就包含了哪些更重要,哪些不重要的信息在里面。
一般情况下$K = V$,在Transformer里,$K!=V$的情况也是可以的,但是$K$和$V$之间一定有联系,这样$Q$和$K$点乘出来的值才是有意义的,才能指导$V$哪些重要哪些不重要。
之后将得到的相似度进行 $softmax$ 操作,进行归一化:
$\alpha_i = \text{softmax}\left(\frac{f(Q, K_i)}{\sqrt{d_k}}\right)$,这里简单讲解除以 $sort(dk)$的作用:假设$Q$,$K$里的元素的均值为0,方差为 1,那么$A^T=Q^TK$中元素的均值为$0$,方差为$d$。当$d$变得很大时,$A$中的元素的方差也会变得很大,如果 A 中的元素方差很大(分布的方差大,分布集中在绝对值大的区域),在数量级较大时,$softmax$将几乎全部的概率分布都分配给了最大值对应的标签,由于某一维度的数量级较大,进而会导致$softmax$未来求梯度时会消失。总结一下就是$softmax(A)$的分布会和$d$有关。因此$A$中每一个元素除$sort(dₖ)$后,方差又变为1,并且$A$的数量级也将会变小。
最后,针对计算出来的权重$a_i$,对$V$中的所有 values 进行加权求和计算,得到 Attention 向量:$\text{Attention}(Q, K, V) = \sum_{i=1}^{m} \text{softmax}\left(\frac{f(Q, K_i)}{\sqrt{d_k}}\right) V_i$